Bayesian Generalized Linear Models with Metropolis-Hastings Algorithm

Published

12 July 2022

Generalized Linear Models

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm, poisson

We are going to take a problem-solving based approach to GLMs. The only conceptual leap you will need to make is the idea of a link function.

Binomial Likelihood

Bot Detection

Suppose you wanted to predict the probability of a twitter account being a bot using common attributes of the account, such as the ratio of followers to following and the lifetime of the account. How would you design this model?

n = 1000
ratio = np.random.exponential(size = n, scale = 1)
lifetime = np.random.exponential(size = n, scale = 1)
nu = 1 - 2 * ratio - lifetime
p = 1 / (1 + np.exp(-nu))
bot = np.random.binomial(p = p, n = 1)

bot.mean()

0.231
\[B_i \sim \text{Bernoulli}(p_i)\] \[\text{logit}( p_i) \sim \beta_0 + \beta_1 R_i + \beta_2 L_i\] \[\beta_0, \beta_1, \beta_2 \sim \text{Normal}(0, 10)\] \[\text{logit}(p_i) = \ln \bigg( \frac{p_i}{1-p_i} \bigg )\] \[\text{inv logit}(\beta_0 + \beta_1 R_i + \beta_2 L_i) = \frac{1}{1 + \exp(-(\beta_0 + \beta_1 R_i + \beta_2 L_i))}\] 
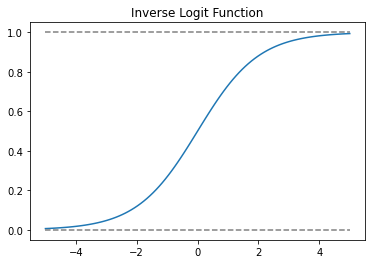
xx = np.linspace(-5, 5, 100)
plt.plot(xx, 1 / (1 + np.exp(-xx)))
plt.plot(xx, np.ones(100), linestyle = '--', color = 'grey')
plt.plot(xx, np.zeros(100), linestyle = '--', color = 'grey')
plt.title('Inverse Logit Function')
plt.show()

png

def inv_logit(x):
    return 1 / (1 + np.exp(-x))
\[\log f(b_i|p_i) = b_i \log p_i + (1 - b_i) \log (1 - p_i)\] 
def prior(b0, b1, b2):


    b0_prior = norm.pdf(x = b0, loc = 0, scale = 10)

    b1_prior = norm.pdf(x = b1, loc = 0, scale = 10)

    b2_prior = norm.pdf(x = b2, loc = 0, scale = 10)

    ######################

    # log probability transforms multiplication to summation

    return np.log(b0_prior) + np.log(b1_prior) + np.log(b2_prior)

 

def likelihood(b0, b1, b2):

     

    nu = b0 + b1 * ratio + b2 * lifetime
    p = inv_logit(nu)
    log_likelihoods = bot * np.log(p) + (1 - bot) * np.log(1 - p)
    ######################

    # log probability transforms multiplication to summation
    return np.sum(log_likelihoods)

 

def posterior(b0, b1, b2):

    return likelihood(b0, b1, b2) + prior(b0, b1, b2)

 

def proposal(b0, b1, b2):

    b0_new = np.random.normal(loc = b0, scale = 0.1)

    b1_new = np.random.normal(loc = b1, scale = 0.1)

    b2_new = np.random.normal(loc = b2, scale = 0.1) 

    return b0_new, b1_new, b2_new

def metropolis(steps):

    beta_steps = np.zeros((steps, 3))
    beta_steps[0, :] = np.zeros(3)


    for step in range(1, steps):              

        b0_old, b1_old, b2_old = beta_steps[step - 1, :]
        
         
        b0_new, b1_new, b2_new = proposal(b0_old, b1_old, b2_old)

        # Use exp to restore from log numbers
        accept_ratio = np.exp(posterior(b0_new, b1_new, b2_new) - posterior(b0_old, b1_old, b2_old))
        ######################
        
        if np.random.uniform(0, 1) < accept_ratio:

            beta_steps[step, :]  = b0_new, b1_new, b2_new

        else:

            beta_steps[step, :]  = b0_old, b1_old, b2_old
            
    return beta_steps

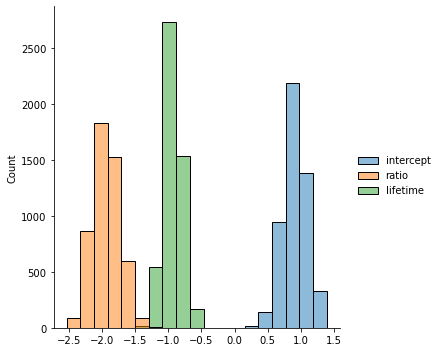
chain1 = metropolis(10000)

chain_df = pd.DataFrame(chain1, columns = ['intercept', 'ratio', 'lifetime'])

sns.displot(chain_df[5000:])

<seaborn.axisgrid.FacetGrid at 0x7f6e20683c70>

png

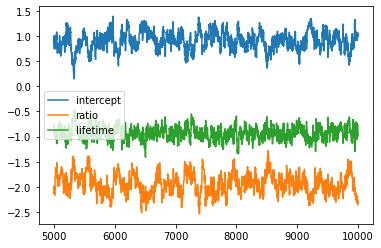
plt.plot(chain_df[5000:])
plt.legend(chain_df.columns)
plt.show()

png

Lefthand Advantage

The data in data(UFClefties) are the outcomes of 205 Ultimate Fighting Championship (UFC) matches. It is widely believed that left-handed fighters (aka “Southpaws”) have an advantage against right-handed fighters, and left-handed men are indeed over-represented among fighters (and fencers and tennis players) compared to the general population. Estimate the average advantage, if any, that a left-handed fighter has against right-handed fighters. Based upon your estimate, why do you think lefthanders are over-represented among UFC fighters?

ufc = pd.read_csv('data/UFCLefties.csv', delimiter = ";")

ufc.head()
fight episode fight.in.episode fighter1.win fighter1 fighter2 fighter1.lefty fighter2.lefty
0 1181 118 1 0 146 175 1 1
1 1182 118 2 0 133 91 1 0
2 1183 118 3 1 56 147 1 0
3 1184 118 4 1 192 104 0 0
4 1185 118 5 1 79 15 0 0
\[W_i \sim \text{Bernoulli}(p_i)\] \[\text{logit} (p_i) = \beta(L_{1[i]} - L_{2[i]})\] 
win = ufc['fighter1.win'].to_numpy()
f1_lefty = ufc['fighter1.lefty'].to_numpy()
f2_lefty = ufc['fighter2.lefty'].to_numpy()

def prior(b):

     

    b_prior = norm.pdf(x = b, loc = 0, scale = 1)

    ######################
    
    # log probability transforms multiplication to summation
    return np.log(b_prior)

def likelihood(b):

     
    nu = b * (f1_lefty - f2_lefty)
    p = inv_logit(nu)

    log_likelihoods = win * np.log(p) + (1 - win) * np.log(1 - p)
    ######################

    # log probability transforms multiplication to summation
    return np.sum(log_likelihoods)

def posterior(b):

    return likelihood(b) + prior(b)

def proposal(b):

    b_new = np.random.normal(loc = b, scale = 0.5)

    return b_new

def metropolis(steps):

    beta_steps = np.zeros(steps)
    beta_steps[0] = 0

    for step in range(1, steps):              

        b_old = beta_steps[step - 1]
        
         
        b_new = proposal(b_old)
        
        # Use exp to restore from log numbers
        accept_ratio = np.exp(posterior(b_new) - posterior(b_old))
        #######################
        
        if np.random.uniform(0, 1) < accept_ratio:

            beta_steps[step]  = b_new

        else:

            beta_steps[step]  = b_old
            
    return beta_steps

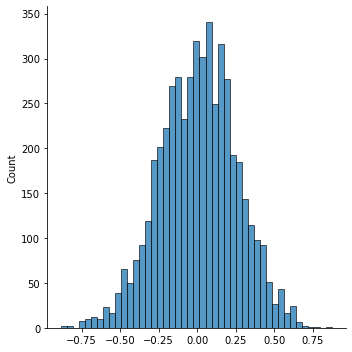
chain1 = metropolis(10000)

sns.displot(chain1[5000:])

<seaborn.axisgrid.FacetGrid at 0x7f6ddfb45d90>

png

plt.plot(chain1)

[<matplotlib.lines.Line2D at 0x7f6ddf77e670>]

png

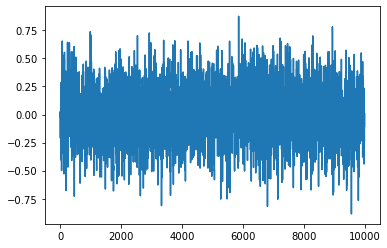
Why does there appear to be no advantage?

n = 1000
lefty = np.random.binomial(n = 1, p = 0.1, size = n)
ability = np.random.normal(size = n)
qualify = np.where((ability > 2) | ((ability > 1.25) & lefty), 1, 0)

(qualify & lefty).sum() / qualify.sum()

0.34375

np.random.seed(420)
k = 2 # importance of ability differences
b_sim = 0.5 # lefty advantage
l = lefty[qualify==1]
a = ability[qualify==1]
M = sum(qualify==1)
mid = int(M/2)
win = np.zeros(mid) # matches
f1_lefty = np.zeros(mid)
f2_lefty = np.zeros(mid)

for i in range(mid):
    a1 = a[i] + b_sim * l[i]
    a2 = a[mid + i] + b_sim * l[mid + i]
    p = inv_logit(k * (a1 - a2))
    f1win = np.random.binomial(n = 1, p = p, size = 1)
    win[i] = f1win
    f1_lefty[i] = l[i]
    f2_lefty[i] = l[mid + i]

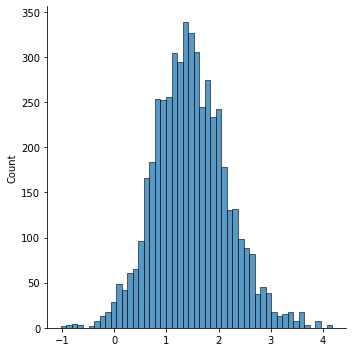
chain1 = metropolis(10000)

sns.displot(chain1[5000:])

<seaborn.axisgrid.FacetGrid at 0x7f6ddf793400>

png

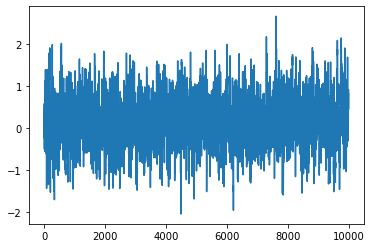
plt.plot(chain1)

[<matplotlib.lines.Line2D at 0x7f6ddf449f70>]

png

Poisson Likelihood

Counting Claims

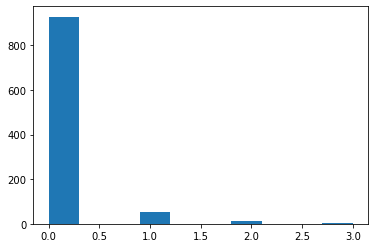
Suppose you wish to estimate the number of automobile claims a policy holder will file over the life of a policy using the driver’s age and credit score (in 00s).

n = 1000
age = np.random.uniform(size = n, low = 16, high = 64)
credit = np.random.uniform(size = n, low = 3, high = 8.5)
nu = 6 - 0.5 * age ** (1/3) - 1.5 * credit
lam = np.exp(nu)
claims = np.random.poisson(lam = lam, size = n)

plt.hist(claims)
plt.show()

png

\[C_i \sim \text{Poisson}(\lambda_i)\] \[\text{ln}( \lambda_i) = \beta_0 + \beta_1 A_i + \beta_2 Cr_i\] 
def prior(b0, b1, b2):

     

    b0_prior = norm.pdf(x = b0, loc = 0, scale = 10)

    b1_prior = norm.pdf(x = b1, loc = 0, scale = 10)

    b2_prior = norm.pdf(x = b2, loc = 0, scale = 10)
    ######################

    # log probability transforms multiplication to summation

    return np.log(b0_prior) + np.log(b1_prior) + np.log(b2_prior)

 

def likelihood(b0, b1, b2):

     

    nu = b0 + b1 * age ** (1/3) + b2 * credit
    lam = np.exp(nu)

    likelihoods = poisson(lam).pmf(claims)
    ######################

    # log probability transforms multiplication to summation
    return np.sum(np.log(likelihoods))

 

def posterior(b0, b1, b2):

    return likelihood(b0, b1, b2) + prior(b0, b1, b2)

 

def proposal(b0, b1, b2):

    b0_new = np.random.normal(loc = b0, scale = 0.01)

    b1_new = np.random.normal(loc = b1, scale = 0.01)

    b2_new = np.random.normal(loc = b2, scale = 0.01) 

    return b0_new, b1_new, b2_new

def metropolis(steps):

    beta_steps = np.zeros((steps, 3))
    beta_steps[0, :] = np.array([5, 0, 0])


    for step in range(1, steps):              


        b0_old, b1_old, b2_old = beta_steps[step - 1, :]
        
         

        b0_new, b1_new, b2_new = proposal(b0_old, b1_old, b2_old)

        # Use exp to restore from log numbers
        accept_ratio = np.exp(posterior(b0_new, b1_new, b2_new) - posterior(b0_old, b1_old, b2_old))
        #########################
        
        if np.random.uniform(0, 1) < accept_ratio:

            beta_steps[step, :]  = b0_new, b1_new, b2_new

        else:

            beta_steps[step, :]  = b0_old, b1_old, b2_old
            
    return beta_steps

chain1 = metropolis(10000)

/tmp/ipykernel_10118/599861409.py:17: RuntimeWarning: overflow encountered in exp
  accept_ratio = np.exp(posterior(b0_new, b1_new, b2_new) - posterior(b0_old, b1_old, b2_old))

chain_df = pd.DataFrame(chain1, columns = ['intercept', 'age', 'credit'])

sns.displot(chain_df[5000:])

<seaborn.axisgrid.FacetGrid at 0x7f6ddfa7c2e0>

png

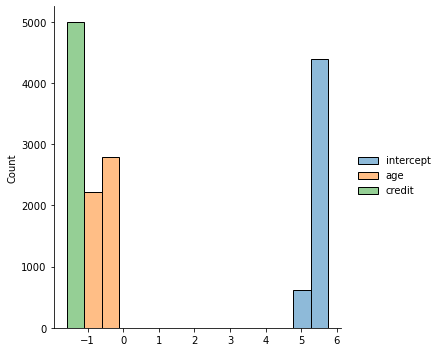
plt.plot(chain_df[5000:])
plt.legend(chain_df.columns)
plt.show()

png

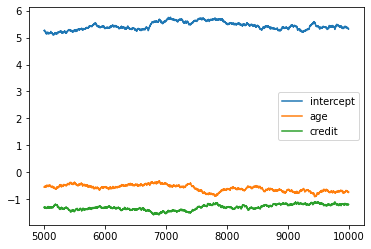
pd.DataFrame(chain1[5000:]).describe()
0 1 2
count 5000.000000 5000.000000 5000.000000
mean 5.429990 -0.596091 -1.310173
std 0.144655 0.119981 0.103329
min 5.097674 -0.915226 -1.590178
25% 5.326552 -0.688531 -1.381540
50% 5.409023 -0.585485 -1.316315
75% 5.531647 -0.497935 -1.217022
max 5.756921 -0.326036 -1.101609

Counting Tools

The island societies of Oceania provide a natural experiment in technological evolution. Different historical island populations possessed tool kits of different size. These kits include fish hooks, axes, boats, hand plows, and many other types of tools. A number of theories predict that larger populations will both develop and sustain more complex tool kits. So the natural variation in population size induced by natural variation in island size in Oceania provides a natural experiment to test these ideas. It’s also suggested that contact rates among populations effectively increase population size, as it’s relevant to technological evolution. So variation in contact rates among Oceanic societies is also relevant.

kline = pd.read_csv('data/kline.csv', delimiter = ';')

kline
culture population contact total_tools mean_TU
0 Malekula 1100 low 13 3.2
1 Tikopia 1500 low 22 4.7
2 Santa Cruz 3600 low 24 4.0
3 Yap 4791 high 43 5.0
4 Lau Fiji 7400 high 33 5.0
5 Trobriand 8000 high 19 4.0
6 Chuuk 9200 high 40 3.8
7 Manus 13000 low 28 6.6
8 Tonga 17500 high 55 5.4
9 Hawaii 275000 low 71 6.6 
tools = kline.total_tools.to_numpy()
log_pop = np.log(kline.population.to_numpy())
contact = kline.contact.apply(lambda x: 1 if x == 'high' else 0).to_numpy()
\[T_i \sim Poisson(\lambda_i)\] \[\ln \lambda_i = \beta_0 + \beta_1 C_i + \beta_2 \log P_i + \beta_3 C_i\log P_i\] 
from scipy.stats import poisson, norm

def prior(b0, b1, b2, b3):
    
     
    b0_prior = norm.pdf(x = b0, loc = 0, scale = 100)
    b1_prior = norm.pdf(x = b1, loc = 0, scale = 1)
    b2_prior = norm.pdf(x = b2, loc = 0, scale = 1)
    b3_prior = norm.pdf(x = b3, loc = 0, scale = 1)
    ######################
    
    # log probability transforms multiplication to summation
    return np.log(b0_prior) + np.log(b1_prior) + np.log(b2_prior) + np.log(b3_prior)

def likelihood(b0, b1, b2, b3):
    
     
    nu = b0 + b1 * contact + b2 * log_pop + b3 * contact * log_pop
    lam = np.exp(nu)
    likelihoods = poisson(lam).pmf(tools)
    ######################
    
    # log probability transforms multiplication to summation
    return np.sum(np.log(likelihoods))

def posterior(b0, b1, b2, b3):
    
    return likelihood(b0, b1, b2, b3) + prior(b0, b1, b2, b3)

def proposal(b0, b1, b2, b3):

    b0_new = np.random.normal(loc = b0, scale = 0.01)
    b1_new = np.random.normal(loc = b1, scale = 0.01)
    b2_new = np.random.normal(loc = b2, scale = 0.01)
    b3_new = np.random.normal(loc = b3, scale = 0.01)

    return b0_new, b1_new, b2_new, b3_new

def metropolis(steps):

    beta_steps = np.zeros((steps, 4))
    beta_steps[0, :] = np.zeros(4)


    for step in range(1, steps):              


        b0_old, b1_old, b2_old, b3_old = beta_steps[step - 1, :]
        
         
        b0_new, b1_new, b2_new, b3_new = proposal(b0_old, b1_old, b2_old, b3_old)


        # Use exp to restore from log numbers
        accept_ratio = np.exp(posterior(b0_new, b1_new, b2_new, b3_new) - posterior(b0_old, b1_old, b2_old, b3_old))
        #########################


        if np.random.uniform(0, 1) < accept_ratio:

            beta_steps[step, :]  = b0_new, b1_new, b2_new, b3_new

        else:

            beta_steps[step, :]  = b0_old, b1_old, b2_old, b3_old
            
    return beta_steps

chain1 = metropolis(20000)

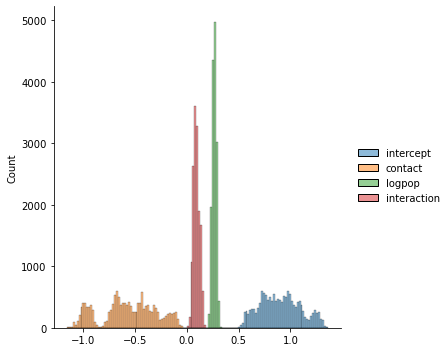
chain_df = pd.DataFrame(chain1, columns = ['intercept', 'contact', 'logpop', 'interaction'])

sns.displot(chain_df.iloc[5000:, :])

<seaborn.axisgrid.FacetGrid at 0x7f6ddf143d60>

png

plt.plot(chain_df.iloc[5000:])
plt.legend(chain_df.columns)
plt.show()

png

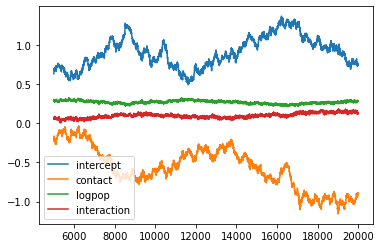
chain_df.iloc[5000:].describe()
intercept contact logpop interaction
count 15000.000000 15000.000000 15000.000000 15000.000000
mean 0.904522 -0.572605 0.267322 0.096037
std 0.195995 0.268268 0.019789 0.030269
min 0.489351 -1.156353 0.210057 0.005709
25% 0.751685 -0.733303 0.253605 0.073918
50% 0.897453 -0.569403 0.267624 0.093761
75% 1.046071 -0.373637 0.281905 0.116540
max 1.363002 -0.032650 0.326950 0.182332

No Contact Simulations

n = 10000
post = chain_df.iloc[-n:, :]
logpop = np.linspace(7, 13, 100)
nc_lower_89 = np.zeros(100)
nc_upper_89 = np.zeros(100)

for i, lp in enumerate(logpop):
    nu = post.intercept + post.logpop * lp
    lam = np.exp(nu)
    tools_sim = np.random.poisson(size = n, lam = lam)
    
    nc_lower_89[i], nc_upper_89[i] = np.quantile(tools_sim, q = (0.055, 1 - 0.055))

Contact Simulations

n = 10000
post = chain_df.iloc[-n:, :]
logpop = np.linspace(7, 13, 100)
c_lower_89 = np.zeros(100)
c_upper_89 = np.zeros(100)

for i, lp in enumerate(logpop):
    nu = post.intercept + post.logpop * lp + chain_df.contact.mean() + post.interaction * lp
    lam = np.exp(nu)
    tools_sim = np.random.poisson(size = n, lam = lam)
    
    c_lower_89[i], c_upper_89[i] = np.quantile(tools_sim, q = (0.055, 1 - 0.055))

kline['log_pop'] = np.log(kline.population)

sns.scatterplot(x = 'log_pop', y = 'total_tools', data = kline, hue = 'contact')

### No Contact
nu = post.intercept.mean() + post.logpop.mean() * logpop
plt.plot(logpop, np.exp(nu), color = "dodgerblue")
plt.fill_between(logpop, nc_upper_89, nc_lower_89, color = "dodgerblue", alpha = 0.5)

### Contact
nu = post.intercept.mean() + post.logpop.mean() * logpop + post.contact.mean() + post.interaction.mean()*logpop
plt.plot(logpop, np.exp(nu), color = "darkorange")
plt.fill_between(logpop, c_upper_89, c_lower_89, color = "darkorange", alpha = 0.5)
plt.show()

png

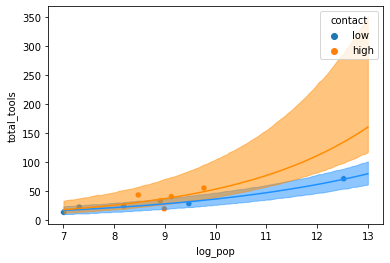
On the natural scale

No Contact Simulations

n = 10000
post = chain_df.iloc[-n:, :]
pop = np.linspace(1000, 275000, 100)
nc_lower_89 = np.zeros(100)
nc_upper_89 = np.zeros(100)

for i, p in enumerate(pop):
    nu = post.intercept + post.logpop * np.log(p)
    lam = np.exp(nu)
    tools_sim = np.random.poisson(size = n, lam = lam)
    
    nc_lower_89[i], nc_upper_89[i] = np.quantile(tools_sim, q = (0.055, 1 - 0.055))

Contact Simulations

n = 10000
post = chain_df.iloc[-n:, :]
pop = np.linspace(1000, 275000, 100)
c_lower_89 = np.zeros(100)
c_upper_89 = np.zeros(100)

for i, p in enumerate(pop):
    nu = post.intercept + post.logpop * np.log(p) + post.contact + post.interaction * np.log(p)
    lam = np.exp(nu)
    tools_sim = np.random.poisson(size = n, lam = lam)
    
    c_lower_89[i], c_upper_89[i] = np.quantile(tools_sim, q = (0.055, 1 - 0.055))

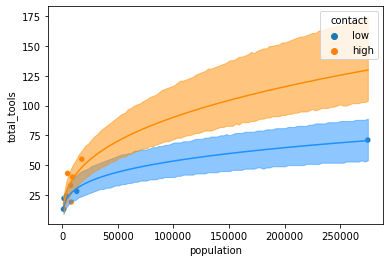
sns.scatterplot(x = 'population', y = 'total_tools', data = kline, hue = 'contact')

### No Contact
nu = chain_df.intercept.mean() + chain_df.logpop.mean() * np.log(pop)
plt.plot(pop, np.exp(nu), color = "dodgerblue")
plt.fill_between(pop, nc_upper_89, nc_lower_89, color = "dodgerblue", alpha = 0.5)

### Contact
nu = chain_df.intercept.mean() + chain_df.logpop.mean() * np.log(pop) + chain_df.contact.mean() + chain_df.interaction.mean()*np.log(pop)
plt.plot(pop, np.exp(nu), color = "darkorange")
plt.fill_between(pop, c_upper_89, c_lower_89, color = "darkorange", alpha = 0.5)
plt.show()

png

Sources:

Statistical Rethinking - Richard McElreath