Tweedie Regression from Scratch with Newton-Raphson and Gradient Boosting
Tweedie Models From Scratch
import tweedie
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
n = 200
x = np.sort(np.random.normal(size = n))
b0 = 0.1
b1 = 1
mu = np.exp(b0 + b1 * x)
# q = np.random.binomial(size = n, p = 0.1, n = 1)
# y = q * tweedie.tweedie(mu=mu, p=1.5, phi=5).rvs(n)
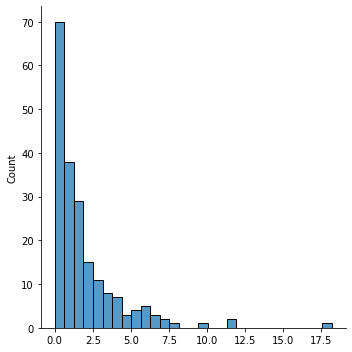
y = tweedie.tweedie(mu=mu, p=1.5, phi=0.5).rvs(n)
sns.displot(y)
<seaborn.axisgrid.FacetGrid at 0x7fc7729eb460>
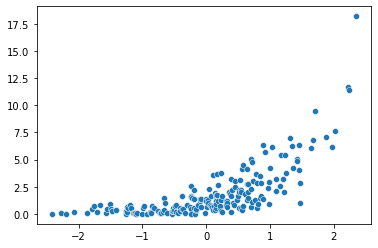
sns.scatterplot(x = x, y = y)
<AxesSubplot:>
pd.DataFrame(y).describe()
| 0 | |
|---|---|
| count | 200.000000 |
| mean | 1.859694 |
| std | 2.359829 |
| min | 0.000000 |
| 25% | 0.415380 |
| 50% | 1.034595 |
| 75% | 2.289224 |
| max | 18.191432 |
Generalized Linear Model
The Newton-Raphson Method
\[\hat \theta_{j+1} = \theta_j - H^{-1} l'(\theta_j)\]where $H$ is the matrix of second derivatives of the log-likelihood with respect to $\theta$ and $l’(\theta_j)$ is the vector of first derivatives.
Here, we treat
\[\theta = \exp \{\beta_0 + \beta_1 x_i \}\]Our log-likelihood is
\[l(\theta) \propto \sum_i y_i \frac{\exp^{1-p} \{\beta_0 + \beta_1 x_i\}}{1 - p} - \frac{\exp^{2-p} \{\beta_0 + \beta_1 x_i \}}{2 - p}\]Our vector of first derivatives
\[\begin{bmatrix} \sum_i y_i \exp^{1-p}\{\beta_0 + \beta_1 x_i\} - \exp^{2-p} \{\beta_0 + \beta_1 x_i \} \\ \sum_i y_i x_i \exp^{1-p}\{\beta_0 + \beta_1 x_i\} - x_i\exp^{2-p} \{\beta_0 + \beta_1 x_i \} \end{bmatrix}\]And our Hessian
\[\begin{bmatrix} \sum_i y_i (1-p) \exp^{1-p}\{\beta_0 + \beta_1 x_i\} - (2-p)\exp^{2-p} \{\beta_0 + \beta_1 x_i \} & \sum_i y_i x_i (1-p) \exp^{p-1}\{\beta_0 + \beta_1 x_i\} - x_i(2-p)\exp^{2-p} \{\beta_0 + \beta_1 x_i \} \\ \sum_i y_i x_i (1-p) \exp^{1-p}\{\beta_0 + \beta_1 x_i\} - x_i (2-p)\exp^{2-p} \{\beta_0 + \beta_1 x_i \} & \sum_i y_i x_i^2 (1-p) \exp^{1-p}\{\beta_0 + \beta_1 x_i\} - x_i^2 (2-p)\exp^{2-p} \{\beta_0 + \beta_1 x_i \} \end{bmatrix}\]Tweedie Generalized Linear Model Algorithm
-
Initialize $\hat\theta_0 = [\hat \beta_0, \hat \beta_1] = [0, 0]$, $\epsilon = ||\theta_j - \theta_{j - 1}||$
-
While $\epsilon < \text{tol}$
a) Compute vector of first derivatives with current parameters
\[\begin{bmatrix} \sum_i y_i \exp^{1-p}\{\beta_0 + \beta_1 x_i\} - \exp^{2-p} \{\beta_0 + \beta_1 x_i \} \\ \sum_i y_i x_i \exp^{1-p}\{\beta_0 + \beta_1 x_i\} - x_i\exp^{2-p} \{\beta_0 + \beta_1 x_i \} \end{bmatrix}\]b) Compute Hessian matrix of second derivatives with current parameters
\[\begin{bmatrix} \sum_i y_i (1-p) \exp^{1-p}\{\beta_0 + \beta_1 x_i\} - (2-p)\exp^{2-p} \{\beta_0 + \beta_1 x_i \} & \sum_i y_i x_i (1-p) \exp^{p-1}\{\beta_0 + \beta_1 x_i\} - x_i(2-p)\exp^{2-p} \{\beta_0 + \beta_1 x_i \} \\ \sum_i y_i x_i (1-p) \exp^{1-p}\{\beta_0 + \beta_1 x_i\} - x_i (2-p)\exp^{2-p} \{\beta_0 + \beta_1 x_i \} & \sum_i y_i x_i^2 (1-p) \exp^{1-p}\{\beta_0 + \beta_1 x_i\} - x_i^2 (2-p)\exp^{2-p} \{\beta_0 + \beta_1 x_i \} \end{bmatrix}\]c) Update
$\hat \theta_{j+1} = \theta_j - H^{-1} l’(\theta_j)$
def first_derivatives(b0, b1, x, y, p):
d_b0 = np.sum(y * np.exp(b0 + b1 * x) ** (1 - p) - np.exp(b0 + b1 * x) ** (2 - p))
d_b1 = np.sum(y * x * np.exp(b0 + b1 * x) ** (1 - p) - x * np.exp(b0 + b1 * x) ** (2 - p))
return np.array([d_b0, d_b1]).reshape(-1, 1)
def hessian(b0, b1, x, y, p):
d_b02 = np.sum(y * (1 - p) * np.exp(b0 + b1 * x) ** (1 - p) - (2 - p) * np.exp(b0 + b1 * x) ** (2 - p))
d_b12 = np.sum(y * x ** 2 * (1 - p) * np.exp(b0 + b1 * x) ** (1 - p) - x ** 2 * (2 - p) * np.exp(b0 + b1 * x) ** (2 - p))
d_b0_b1 = np.sum(y * x * (1 - p) * np.exp(b0 + b1 * x) ** (1 - p) - x * (2 - p) * np.exp(b0 + b1 * x) ** (2 - p))
return np.array([[d_b02, d_b0_b1],
[d_b0_b1, d_b12]])
n = 10
params = np.zeros((n, 2))
for i in range(1, n):
b0, b1 = params[i - 1]
p = 1.5
### Compute vector of first derivates
d_l = first_derivatives(b0, b1, x, y, p)
### Compute matrix of hessians
h = hessian(b0, b1, x, y, p)
h_inv = np.linalg.inv(h)
### Update current parameters
update = h_inv.dot(d_l).flatten()
params[i] = params[i - 1] - update
params
array([[0. , 0. ],
[0.11205264, 0.80582605],
[0.11354877, 1.0289923 ],
[0.11374388, 1.03153549],
[0.11374394, 1.03153548],
[0.11374394, 1.03153548],
[0.11374394, 1.03153548],
[0.11374394, 1.03153548],
[0.11374394, 1.03153548],
[0.11374394, 1.03153548]])
plt.scatter(x, y)
plt.plot(x, np.exp(0.03 + 0.98 * x), color = 'orange')
plt.show()

Gradient Boosting Machines
Recursively fit a decision tree to the negative gradient of the tweedie deviance of the current predictions to the observed values
Recall the general GBM algorithm

The algorithm in words:
-
Start out with an initial prediction (the mean).
-
Compute the ‘residuals’ with this prediction.
-
Fit a simple decision tree to the ‘residuals’. This decision tree minimizes the MSE.
-
Compute the optimal node value for each of the partitions given by the simple decision tree.
-
Update the current predictions and go back to step 2.
Our loss function is the tweedie deviance
\[L(\mu, y) = 2 \left(\frac{\max(0, y)^{2-p}}{(1-p)(2-p)} - \frac{y\mu^{1-p}}{1-p} + \frac{\mu^{2-p}}{2-p} \right)\]Here we treat
\[\mu = \exp(f(X))\] \[L(\mu, y) = 2 \left(\frac{\max(0, y)^{2-p}}{(1-p)(2-p)} - \frac{y\exp(f(X))^{1-p}}{1-p} + \frac{\exp(f(X))^{2-p}}{2-p} \right)\]With gradient
\[\frac{\delta L(\mu, y)}{\delta \mu} = \exp(f(X))^{(1-p)} * (\exp(f(X)) - y)\]At the terminal nodes we solve for
\[\arg \min_\gamma \sum_{x_i \in R_{j, m}} L(y_i, \exp(f_{m - 1}(x_i) + \gamma))\] \[\gamma_{j, m} = \log \frac{\sum_{x_i \in R_{j, m}} y_i}{\sum_{x_i \in R_{j, m}} \exp(f_{m - 1}(x_i))}\]Updated predictions are
\[f_m(x) = f_{m - 1}(x) + \nu \sum \gamma_{j, m}I(x \in R_{j, m})\]Tweedie Gradient Boosting Algorithm
-
Initialize $f_0(x) = \bar y$
-
For $m=1$ to $M$
a) For $i = 1, …, N$ compute
$r_{im} = \exp(f(x_i))^{(1-p)}(\exp(f(x_i)) - y)$
b) Fit a regression tree to $r_{im}$
c) For $j = 1, …, J_m$ compute
$\gamma_{j, m} = \log \frac{\sum_{x_i \in R_{j, m}} y_i}{\sum_{x_i \in R_{j, m}} \exp(f_{m - 1}(x_i))}$
d) Update
$f_m(x) = f_{m - 1}(x) + \nu \sum \gamma_{j, m}I(x \in R_{j, m})$
def tweedie_grad(y, mu, p = 1.5):
return np.exp(mu) ** (1 - p) * (np.exp(mu) - y)
def tweedie_deviance(y_pred, y_true, p = 1.5):
# Requires y_pred > 0 and y_true >= 0
y_pred = np.exp(y_pred)
dev = 2 * (
np.power(y_true, 2 - p) / ((1 - p) * (2 - p))
- y_true * np.power(y_pred, (1 - p)) / (1 - p)
+ np.power(y_pred, (2 - p)) / (2 - p)
)
return np.mean(dev)
def fit_weak_tree(X, psuedo_r):
weak_tree = tree.DecisionTreeRegressor(max_depth = 2)
weak_tree.fit(X, psuedo_r)
terminal_regions = weak_tree.apply(X)
return weak_tree, terminal_regions
def assign_terminal_node_values(terminal_regions, y, current_predictions):
possible_regions = np.unique(terminal_regions)
gammas = np.zeros(len(y))
for region in possible_regions:
in_terminal_region = region == terminal_regions
y_in_node = y[in_terminal_region]
current_predictions_in_node = current_predictions[in_terminal_region]
gammas[in_terminal_region] = max(np.log(np.sum(y_in_node) / np.sum(np.exp(current_predictions_in_node))), -20)
return gammas
from sklearn import tree
### Params
max_trees = 500
learn_rate = 0.1
### Initial Predictions
F0 = np.log(np.mean(y))
current_predictions = np.repeat(F0, len(y))
psuedo_r = tweedie_grad(y, current_predictions)
X = x.reshape(-1, 1)
### Initial Loss
tweedie_loss = [None for i in range(max_trees + 1)]
tweedie_loss[0] = tweedie_deviance(current_predictions, y)
for T in range(1, max_trees + 1):
### Fit weak tree to psuedo residuals
current_tree, current_terminal_regions = fit_weak_tree(X, psuedo_r)
### Compute Terminal Node Values
gammas = assign_terminal_node_values(current_terminal_regions, y, current_predictions)
### Update Predictions
current_predictions += learn_rate * gammas
### Psuedo Residuals (negative gradient)
psuedo_r = tweedie_grad(y, current_predictions)
### Track Loss
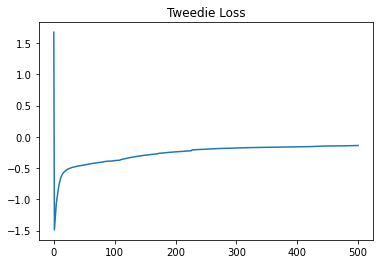
tweedie_loss[T] = -tweedie_deviance(current_predictions, y)
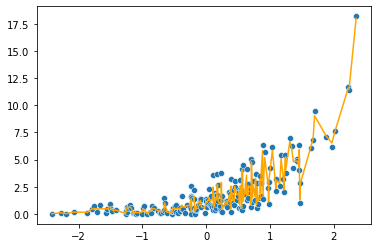
sns.scatterplot(x = x, y = y)
plt.plot(x, np.exp(current_predictions), color = 'orange')
plt.figure()
plt.title('Tweedie Loss')
plt.plot(tweedie_loss)
plt.show()